We first study the bounded mean oscillation of planar harmonic mappings. Then we establish a relationship between Lipschitz-type spaces and equivalent modulus of real harmonic mappings. Finally, we obtain sharp estimates on the Lipschitz number of planar harmonic mappings in terms of the bounded mean oscillation norm, which shows that the harmonic Bloch space is isomorphic to 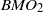 $BM{O}_{2} $ as a Banach space.
$BM{O}_{2} $ as a Banach space.