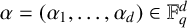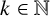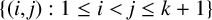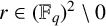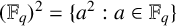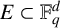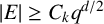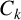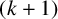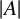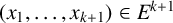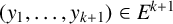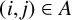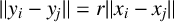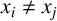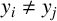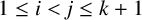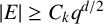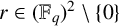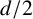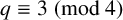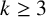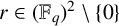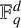Let 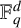 $\mathbb {F}_q^d$ denote the d-dimensional vector space over the finite field
$\mathbb {F}_q^d$ denote the d-dimensional vector space over the finite field 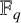 $\mathbb {F}_q$ with q elements. Define
$\mathbb {F}_q$ with q elements. Define 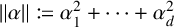 for
for 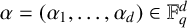 $\alpha = (\alpha _1, \dots , \alpha _d) \in \mathbb {F}_q^d$. Let
$\alpha = (\alpha _1, \dots , \alpha _d) \in \mathbb {F}_q^d$. Let 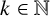 $k\in \mathbb {N}$, A be a nonempty subset of
$k\in \mathbb {N}$, A be a nonempty subset of 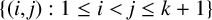 $\{(i, j): 1 \leq i < j \leq k + 1\}$ and
$\{(i, j): 1 \leq i < j \leq k + 1\}$ and 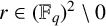 $r\in (\mathbb {F}_q)^2\setminus {0}$, where
$r\in (\mathbb {F}_q)^2\setminus {0}$, where 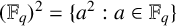 $(\mathbb {F}_q)^2=\{a^2:a\in \mathbb {F}_q\}$. If
$(\mathbb {F}_q)^2=\{a^2:a\in \mathbb {F}_q\}$. If 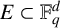 $E\subset \mathbb {F}_q^d$, our main result demonstrates that when the size of the set E satisfies
$E\subset \mathbb {F}_q^d$, our main result demonstrates that when the size of the set E satisfies 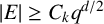 $|E| \geq C_k q^{d/2}$, where
$|E| \geq C_k q^{d/2}$, where 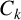 $C_k$ is a constant depending solely on k, it is possible to find two
$C_k$ is a constant depending solely on k, it is possible to find two 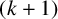 $(k+1)$-tuples in E such that one of them is dilated by r with respect to the other, but only along
$(k+1)$-tuples in E such that one of them is dilated by r with respect to the other, but only along 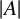 $|A|$ edges. To be more precise, we establish the existence of
$|A|$ edges. To be more precise, we establish the existence of 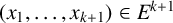 $(x_1, \dots , x_{k+1}) \in E^{k+1}$ and
$(x_1, \dots , x_{k+1}) \in E^{k+1}$ and 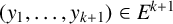 $(y_1, \dots , y_{k+1}) \in E^{k+1}$ such that, for
$(y_1, \dots , y_{k+1}) \in E^{k+1}$ such that, for 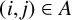 $(i, j) \in A$, we have
$(i, j) \in A$, we have 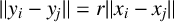 $\lVert y_i - y_j \rVert = r \lVert x_i - x_j \rVert $, with the conditions that
$\lVert y_i - y_j \rVert = r \lVert x_i - x_j \rVert $, with the conditions that 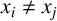 $x_i \neq x_j$ and
$x_i \neq x_j$ and 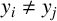 $y_i \neq y_j$ for
$y_i \neq y_j$ for 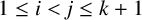 $1 \leq i < j \leq k + 1$, provided that
$1 \leq i < j \leq k + 1$, provided that 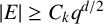 $|E| \geq C_k q^{d/2}$ and
$|E| \geq C_k q^{d/2}$ and 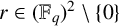 $r\in (\mathbb {F}_q)^2\setminus \{0\}$. We provide two distinct proofs of this result. The first uses the technique of group actions, a powerful method for addressing such problems, while the second is based on elementary combinatorial reasoning. Additionally, we establish that in dimension 2, the threshold
$r\in (\mathbb {F}_q)^2\setminus \{0\}$. We provide two distinct proofs of this result. The first uses the technique of group actions, a powerful method for addressing such problems, while the second is based on elementary combinatorial reasoning. Additionally, we establish that in dimension 2, the threshold 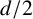 $d/2$ is sharp when
$d/2$ is sharp when 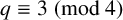 $q \equiv 3 \pmod 4$. As a corollary of the main result, by varying the underlying set A, we determine thresholds for the existence of dilated k-cycles, k-paths and k-stars (where
$q \equiv 3 \pmod 4$. As a corollary of the main result, by varying the underlying set A, we determine thresholds for the existence of dilated k-cycles, k-paths and k-stars (where 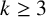 $k \geq 3$) with a dilation ratio of
$k \geq 3$) with a dilation ratio of 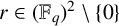 $r\in (\mathbb {F}_q)^2\setminus \{0\}$. These results improve and generalise the findings of Xie and Ge [‘Some results on similar configurations in subsets of
$r\in (\mathbb {F}_q)^2\setminus \{0\}$. These results improve and generalise the findings of Xie and Ge [‘Some results on similar configurations in subsets of 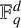 $\mathbb {F}_q^d$’, Finite Fields Appl. 91 (2023), Article no. 102252, 20 pages].
$\mathbb {F}_q^d$’, Finite Fields Appl. 91 (2023), Article no. 102252, 20 pages].
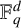 $\mathbb {F}_q^d$
$\mathbb {F}_q^d$


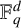
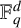
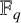
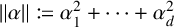 for
for