We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Linear differential algebraic groups (LDAGs) measure differential algebraic dependencies among solutions of linear differential and difference equations with parameters, for which LDAGs are Galois groups. Differential representation theory is a key to developing algorithms computing these groups. In the rational representation theory of algebraic groups, one starts with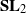 
and tori to develop the rest of the theory. In this paper, we give an explicit description of differential representations of tori and differential extensions of irreducible representation of 
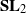. In these extensions, the two irreducible representations can be non-isomorphic. This is in contrast to differential representations of tori, which turn out to be direct sums of isotypic representations.
