We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We show that the diameter of a uniformly drawn spanning tree of a simple connected graph on n vertices with minimal degree linear in n is typically of order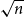 
$\sqrt{n}$
. A byproduct of our proof, which is of independent interest, is that on such graphs the Cheeger constant and the spectral gap are comparable.
