We construct two families of few-weight codes for the Lee weight over the ring
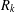 $R_{k}$
based on two different defining sets. For the first defining set, taking the Gray map, we obtain an infinite family of binary two-weight codes which are in fact
$R_{k}$
based on two different defining sets. For the first defining set, taking the Gray map, we obtain an infinite family of binary two-weight codes which are in fact
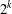 $2^{k}$
-fold replicated MacDonald codes. For the second defining set, we obtain two infinite families of few-weight codes. These few-weight codes can be used to implement secret-sharing schemes.
$2^{k}$
-fold replicated MacDonald codes. For the second defining set, we obtain two infinite families of few-weight codes. These few-weight codes can be used to implement secret-sharing schemes.
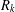 $R_{k}$
$R_{k}$