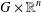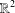We introduce the notion of the equivariant covering type of a space X on which a finite group G acts and study its properties. The equivariant covering type measures the size of G-equivariant good covers of X and is thus an extension of the covering type of a space, introduced by Karoubi and Weibel. We show that the equivariant covering type is a G-homotopy invariant and describe its relation with other G-invariants, like the equivariant LS-category, G-genus, and the multiplicative structures of equivariant cohomology theories. We also compute the G-covering type of regular G-graphs, give estimates for orientation-preserving actions on surfaces and for the projectivizations of complex representations of G and cohomology spheres. As an application, we derive estimates of sizes of minimal G-triangulations for various G-spaces.

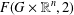The Lusternik–Schnirelmann category cat and topological complexity TC are related homotopy invariants. The topological complexity TC has applications to the robot motion planning problem. We calculate the Lusternik–Schnirelmann category and topological complexity of the ordered configuration space of two distinct points in the product $G\times \mathbb{R}^{n}$ and apply the results to the planar and spatial motion of two rigid bodies in $\mathbb{R}^{2}$ and $\mathbb{R}^{3}$ respectively.