The distribution theory for discrete-time renewal–reward processes with dependent rewards is developed through the derivation of double transforms. By dependent, we mean the more realistic setting in which the reward for an interarrival period is dependent on the duration of the associated interarrival time. The double transforms are the generating functions in time of the time-dependent reward probability-generating functions. Residue and saddlepoint approximations are used to invert such double transforms so that the reward distribution at arbitrary time n can be accurately approximated. In addition, double transforms are developed for the first-passage time distribution that the cumulative reward exceeds a fixed threshold amount. These distributions are accurately approximated by inverting the double transforms using residue and saddlepoint approximation methods. The residue methods also provide asymptotic expansions for moments and allow for the proof of central limit theorems related to these first passage times and reward amounts.

A transient cumulative process based upon a sequence of possibly infinite lifetimes is defined, and examples of such a process are described. Given a mild condition on the improper lifetime distribution and given that all lifetimes observed by time t are finite, the expected value of this transient process at t is related to the expected value of a cumulative process based upon proper lifetimes. This relationship is exploited to show that the conditional behavior of the transient process is analogous to that of a proper process and, in particular, the transient process is asymptotically normal.

The problem of Monte Carlo estimation of M(t) = EN(t), the expected number of renewals in [0, t] for a renewal process with known interarrival time distribution F, is considered. Several unbiased estimators which compete favorably with the naive estimator, N(t), are presented and studied. An approach to reduce the variance of the Monte Carlo estimator is developed and illustrated.

We introduce a versatile class of point processes on the real line, which are closely related to finite-state Markov processes. Many relevant probability distributions, moment and correlation formulas are given in forms which are computationally tractable. Several point processes, such as renewal processes of phase type, Markov-modulated Poisson processes and certain semi-Markov point processes appear as particular cases. The treatment of a substantial number of existing probability models can be generalized in a systematic manner to arrival processes of the type discussed in this paper.

Several qualitative features of point processes, such as certain types of fluctuations, grouping, interruptions and the inhibition of arrivals by bunch inputs can be modelled in a way which remains computationally tractable.

Let {Nt}t >0 be a renewal counting process (cf. Parzen (1962), p. 160) with underlying failure times 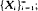let 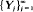be a sequence of non-negative random variables and {Zt}t >0 an associated cumulative process, i.e. 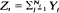if Nt = 1, 2, …, and Zt = 0, if Nt = 0. By convention set Z0 = 0. Consider 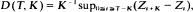the maximum increment of the process {Zt}t >0 in [0, T] over a time K, 0 < K < T, divided by K. Under appropriate conditions it is shown that for a wide range of numbers a there exist constants C(a), uniquely determined by a and the distributions of the Xi's and Yj's, such that D(T, C log T) converges to a with probability 1. This result provides a renewal theoretic variant of Erdös and Rényi's (1970) ‘new law of large numbers’.

For the generalized single server queueing system described herein weak convergence results are obtained for the processes {Wa, n ≧ 0}, {W(t), t ≧ 0}, and {Q (t), t ≧ 0}, where Wn is the waiting time of customer n, W(t) is the workload of the server at time t, and Q(t) is the number of customers present in the system at time t. We also provide a functional strong law, a functional central limit theorem, and a functional law of the iterated logarithm for various cumulative processes in the system.