There is a balance between the amount of (weak) indestructibility one can have and the amount of strong cardinals. It’s consistent relative to large cardinals to have lots of strong cardinals and all of their degrees of strength are weakly indestructible. But this necessitates the destructibility of the partially strong cardinals. Guaranteeing the indestructibility of the partially strong cardinals is shown to be harder. In particular, this work establishes an equiconsistency between:

1. 1. a proper class of cardinals that are strong reflecting strongs; and

2. 2. weak indestructibility for (κ+2)-strength for all cardinals κ in the presence of a proper class of strong cardinals.

1. 3. weak indestructibility for all degrees of strength for a proper class of strong cardinals.

One direction of the equiconsistency of (1) and (2) is proven using forcing and the other using core model techniques from inner model theory. Additionally, connections between weak indestructibility and the reflection properties associated with Woodin cardinals are discussed, and similar results are derived for supercompacts and supercompacts reflecting supercompacts.

Abstract prepared by James Holland.

E-mail: [email protected]

URL: https://sites.math.rutgers.edu/~jch258/assets/dis.pdf

We establish an equiconsistency between (1) weak indestructibility for all $\kappa +2$-degrees of strength for cardinals $\kappa $ in the presence of a proper class of strong cardinals, and (2) a proper class of cardinals that are strong reflecting strongs. We in fact get weak indestructibility for degrees of strength far beyond $\kappa +2$, well beyond the next inaccessible limit of measurables (of the ground model). One direction is proven using forcing and the other using core model techniques from inner model theory. Additionally, connections between weak indestructibility and the reflection properties associated with Woodin cardinals are discussed. This work is a part of my upcoming thesis [7].

We generalise the α-Ramsey cardinals introduced in Holy and Schlicht (2018) for cardinals α to arbitrary ordinals α, and answer several questions posed in that paper. In particular, we show that α-Ramseys are downwards absolute to the core model K for all α of uncountable cofinality, that strategic ω-Ramsey cardinals are equiconsistent with remarkable cardinals and that strategic α-Ramsey cardinals are equiconsistent with measurable cardinals for all α > ω. We also show that the n-Ramseys satisfy indescribability properties and use them to provide a game-theoretic characterisation of completely ineffable cardinals, as well as establishing further connections between the α-Ramsey cardinals and the Ramsey-like cardinals introduced in Gitman (2011), Feng (1990), and Sharpe and Welch (2011).

If M is a proper class inner model of ZFC and $\omega _2^{\bf{M}} = \omega _2 $, then every sound mouse projecting to ω and not past 0¶ belongs to M. In fact, under the assumption that 0¶ does not belong to M, ${\bf{K}}^{\bf{M}} \parallel \omega _2 $ is universal for all countable mice in V.

Similarly, if M is a proper class inner model of ZFC, δ > ω1 is regular, (δ+)M = δ+ and in V there is no proper class inner model with a Woodin cardinal, then ${\bf{K}}^{\bf{M}} \parallel \delta $ is universal for all mice in V of cardinality less than δ.

We determine exact consistency strengths for various failures of the Singular Cardinals Hypothesis (SCH) in the setting of the Zermelo-Fraenkel axiom system ZF without the Axiom of Choice (AC). By the new notion of parallel Prikry forcing that we introduce, we obtain surjective failures of SCH using only one measurable cardinal, including a surjective failure of Shelah's pcf theorem about the size of the power set of ℵω. 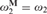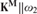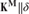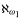Using symmetric collapses to ℵω, , or 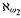, we show that injective failures at ℵω, , or can have relatively mild consistency strengths in terms of Mitchell orders of measurable cardinals. Injective failures of both the aforementioned theorem of Shelah and Silver's theorem that GCH cannot first fail at a singular strong limit cardinal of uncountable cofinality are also obtained. Lower bounds are shown by core model techniques and methods due to Gitik and Mitchell.

We obtain an equiconsistency for a weak form of universal indestructibility for strongness. The equiconsistency is relative to a cardinal weaker in consistency strength than a Woodin cardinal, Stewart Baldwin's notion of hyperstrong cardinal. We also briefly indicate how our methods are applicable to universal indestructibility for supercompactness and strong compactness.