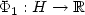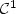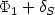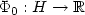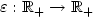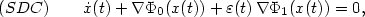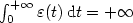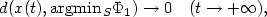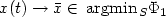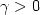A self-consistent model for charged particles, accounting for quantum confinement, diffusive transport and electrostatic interaction is considered. The electrostatic potential is a solution of a three-dimensional Poisson equation with the particle density as the source term. This density is the product of a two-dimensional surface density and that of a one-dimensional mixed quantum state. The surface density is the solution of a drift–diffusion equation with an effective surface potential deduced from the fully three-dimensional one and which involves the diagonalization of a one-dimensional Schrödinger operator. The overall problem is viewed as a two-dimensional drift–diffusion equation coupled to a Schrödinger–Poisson system. The latter is proven to be well posed by a convex minimization technique. A relative entropy and an a priori $L^2$ estimate provide sufficient bounds to prove existence and uniqueness of a global-in-time solution. In the case of thermodynamic equilibrium boundary data, a unique stationary solution is proven to exist. The relative entropy allows us to prove the convergence of the transient solution towards it as time grows to infinity. Finally, the low-order approximation of the relative entropy is used to prove that this convergence is exponential in time.

Let H be a real Hilbert space, $\Phi_1: H\to \xR$ 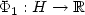a convex function of class ${\mathcal C}^1$ 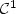that we wish to minimize under the convexconstraint S.A classical approach consists in following the trajectories of the generalizedsteepest descent system (cf.   Brézis [CITE]) appliedto the non-smooth function  $\Phi_1+\delta_S$ 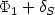. Following Antipin [1], it is also possible to use a continuous gradient-projection system.We propose here an alternative method as follows:given a smooth convex function  $\Phi_0: H\to \xR$ 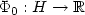whose critical points coincidewith Sand a control parameter $\varepsilon:\xR_+\to \xR_+$ 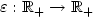tending to zero,we consider the “Steepest Descent and Control” system \[(SDC) \qquad \dot{x}(t)+\nabla \Phi_0(x(t))+\varepsilon(t)\, \nabla \Phi_1(x(t))=0,\] 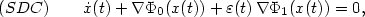where the control ε satisfies $\int_0^{+\infty} \varepsilon(t)\, {\rm d}t =+\infty$ 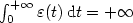. This last condition ensures that ε “slowly” tends to 0. When H is finite dimensional, we then prove that $d(x(t), {\rm argmin}\kern 0.12em_S \Phi_1) \to 0\quad (t\to +\infty),$ 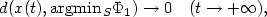and we give sufficient conditions under which  $x(t) \to \bar{x}\in \,{\rm argmin}\kern 0.12em_S \Phi_1$ 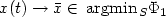.We end the paper by numerical experiments allowing to compare the (SDC) system with the other systems already mentioned.

Let Φ : H → R be a C 2 function on a real Hilbert space and ∑ ⊂ H x R the manifold defined by ∑ := Graph (Φ). We study the motion of a material point with unit mass, subjected to stay on Σ and which moves under the action of the gravity force(characterized by g>0), the reaction force and the friction force ( $\gamma>0$ is the friction parameter). For any initial conditions at time t=0, we prove the existence of a trajectory x(.) defined on R +. We are then interested in the asymptotic behaviour of the trajectories when t → +∞. More precisely, we prove the weak convergence of the trajectories when Φ is convex. When Φ admits a strong minimum, we show moreover that the mechanical energy exponentially decreases to its minimum.