We examine the degree structure $\operatorname {\mathrm {\mathbf {ER}}}$ of equivalence relations on $\omega $ under computable reducibility. We examine when pairs of degrees have a least upper bound. In particular, we show that sufficiently incomparable pairs of degrees do not have a least upper bound but that some incomparable degrees do, and we characterize the degrees which have a least upper bound with every finite equivalence relation. We show that the natural classes of finite, light, and dark degrees are definable in $\operatorname {\mathrm {\mathbf {ER}}}$. We show that every equivalence relation has continuum many self-full strong minimal covers, and that $\mathbf {d}\oplus \mathbf {\operatorname {\mathrm {\mathbf {Id}}}_1}$ needn’t be a strong minimal cover of a self-full degree $\mathbf {d}$. Finally, we show that the theory of the degree structure $\operatorname {\mathrm {\mathbf {ER}}}$ as well as the theories of the substructures of light degrees and of dark degrees are each computably isomorphic with second-order arithmetic.

We study computably enumerable equivalence relations (ceers), under the reducibility $R \le S$ if there exists a computable function f such that 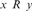$x\,R\,y$ if and only if 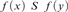$f\left( x \right)\,\,S\,f\left( y \right)$, for every 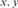$x,y$. We show that the degrees of ceers under the equivalence relation generated by 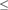$\le$ form a bounded poset that is neither a lower semilattice, nor an upper semilattice, and its first-order theory is undecidable. We then study the universal ceers. We show that 1) the uniformly effectively inseparable ceers are universal, but there are effectively inseparable ceers that are not universal; 2) a ceer R is universal if and only if 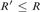$R\prime \le R$, where 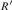$R\prime$ denotes the halting jump operator introduced by Gao and Gerdes (answering an open question of Gao and Gerdes); and 3) both the index set of the universal ceers and the index set of the uniformly effectively inseparable ceers are ${\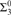rm{\Sigma }}_3^0$-complete (the former answering an open question of Gao and Gerdes).