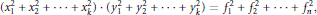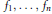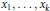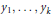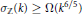1 results
An Asymptotic Bound on the Composition Number of Integer Sums of Squares Formulas
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 1 / 01 March 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 70-79
- Print publication:
- 01 March 2013
-
- Article
-
- You have access
- Export citation
-
Let
${{\sigma }_{\mathbb{Z}}}\left( k \right)$ be the smallest 
$n$ such that there exists an identity with
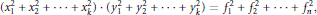$$\left( x_{1}^{2}\,+\,x_{2}^{2}\,+\,\cdot \cdot \cdot \,+\,x_{k}^{2} \right)\,\cdot \,\left( y_{1}^{2}\,+\,y_{2}^{2}\,+\,\cdot \cdot \cdot \,+\,y_{k}^{2} \right)\,=\,f_{1}^{2}\,+\,f_{2}^{2}\,+\,\cdot \cdot \cdot \,+\,f_{n}^{2},$$
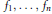${{f}_{1}},...,\,{{f}_{n}}$ being polynomials with integer coefficients in the variables 
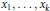${{x}_{1}},...,\,{{x}_{k}}$ and 
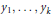${{y}_{1}},...,\,{{y}_{k}}$. We prove that 
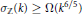${{\sigma }_{\mathbb{Z}}}\left( k \right)\,\ge \,\Omega \left( {{k}^{{6}/{5}\;}} \right)$.
