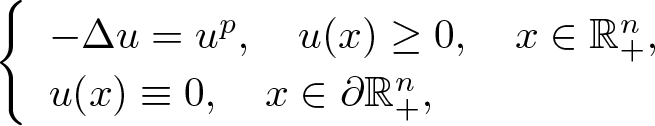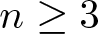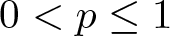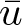In this article, we study the following Dirichlet problem to the sub-linear Lane–Emden equation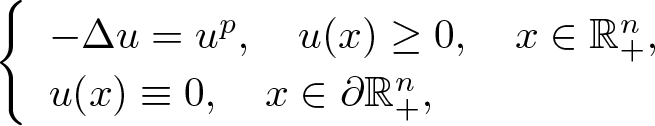

\begin{equation*}\left\{\begin{array}{ll}-\Delta u=u^{p},\quad u(x)\geq0,\quad x\in\mathbb{R}^n_+, \\u(x)\equiv0,\quad x\in\partial\mathbb{R}^n_+,\end{array}\right.\end{equation*}

where 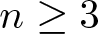$n\geq3$, 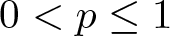$0 \lt p\leq1$. By establishing an equivalent integral equation, we give a lower bound of the Kelvin transformation 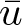$\bar{u}$. Then, by constructing a new comparison function, we apply the maximum principle based on comparisons and the method of moving planes to obtain that u only depends on xn. Based on this, we prove the non-existence of non-negative solutions.

It has been shown by Kesavan (Proc. R. Soc. Edinb. A (133) (2003), 617–624) that the first eigenvalue for the Dirichlet Laplacian in a punctured ball, with the puncture having the shape of a ball, is maximum if and only if the balls are concentric. Recently, Emamizadeh and Zivari-Rezapour (Proc. Am. Math. Soc.136 (2007), 1325–1331) have tried to generalize this result to the case of the p-Laplacian but could succeed only in proving a domain monotonicity result for a weighted eigenvalue problem in which the weights need to satisfy some artificial conditions. In this paper we generalize the result of Kesavan to the case of the p-Laplacian (1 < p < ∞) without any artificial restrictions, and in the process we simplify greatly the proof, even in the case of the Laplacian. The uniqueness of the maximizing domain in the nonlinear case is still an open question.