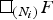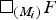1 results
Coarse fundamental groups and box spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1139-1154
- Print publication:
- June 2020
-
- Article
- Export citation
-
We use a coarse version of the fundamental group first introduced by Barcelo, Kramer, Laubenbacher and Weaver to show that box spaces of finitely presented groups detect the normal subgroups used to construct the box space, up to isomorphism. As a consequence, we have that two finitely presented groups admit coarsely equivalent box spaces if and only if they are commensurable via normal subgroups. We also provide an example of two filtrations (Ni) and (Mi) of a free group F such that Mi > Ni for all i with [Mi:Ni] uniformly bounded, but with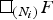
$\squ _{(N_i)}F$ not coarsely equivalent to 
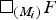$\squ _{(M_i)}F$. Finally, we give some applications of the main theorem for rank gradient and the first ℓ2 Betti number, and show that the main theorem can be used to construct infinitely many coarse equivalence classes of box spaces with various properties.
