We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A chordal graph is a graph with no induced cycles of length at least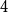 
$4$. Let 
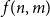$f(n,m)$ be the maximal integer such that every graph with 
$n$ vertices and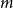 
$m$ edges has a chordal subgraph with at least 
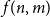$f(n,m)$ edges. In 1985 Erdős and Laskar posed the problem of estimating 
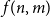$f(n,m)$. In the late 1980s, Erdős, Gyárfás, Ordman and Zalcstein determined the value of 
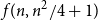$f(n,n^2/4+1)$ and made a conjecture on the value of 
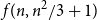$f(n,n^2/3+1)$. In this paper we prove this conjecture and answer the question of Erdős and Laskar, determining 
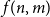$f(n,m)$ asymptotically for all 
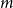$m$ and exactly for 
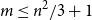$m \leq n^2/3+1$.
