We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider a Keller–Segel model that describes the cellular chemotactic movement away from repulsive chemical subject to logarithmic sensitivity function over a confined region 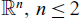in 
${{\mathbb{R}}^n},\,n \le 2$
. This sensitivity function describes the empirically tested Weber–Fecher’s law of living organism’s perception of a physical stimulus. We prove that, regardless of chemotaxis strength and initial data, this repulsive system is globally well-posed and the constant solution is the global and exponential in time attractor. Our results confirm the ‘folklore’ that chemorepulsion inhibits the formation of non-trivial steady states within the logarithmic chemotaxis model, hence preventing cellular aggregation therein.
