In this paper, we prove that cyclic homology, topological cyclic homology, and algebraic 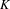 $K$-theory satisfy a pro Mayer–Vietoris property with respect to abstract blow-up squares of varieties, in both zero and finite characteristic. This may be interpreted as the well-definedness of
$K$-theory satisfy a pro Mayer–Vietoris property with respect to abstract blow-up squares of varieties, in both zero and finite characteristic. This may be interpreted as the well-definedness of 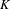 $K$-theory with compact support.
$K$-theory with compact support.
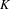 $K$-THEORY
$K$-THEORY