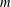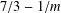We analyse a parallel (identical) machine scheduling problem with job delivery to a single customer. For this problem, each job needs to be processed on $m$ parallel machines non-pre-emptively and then transported to a customer by one vehicle with a limited physical capacity. The optimization goal is to minimize the makespan, the time at which all the jobs are processed and delivered and the vehicle returns to the machine. We present an approximation algorithm with a tight worst-case performance ratio of $7/3-1/m$ for the general case, $m\geq 3$.

We study the best achievable performance (in terms of the average queue size and delay) in a stochastic and dynamic version of the bin-packing problem. Items arrive to a queue according to a Poisson process with rate 2ρ, where ρ ∈ (0, 1). The item sizes are independent and identically distributed (i.i.d.) with a uniform distribution in [0, 1]. At each time unit, a single unit-size bin is available and can receive any of the queued items, as long as their total size does not exceed 1. Coffman and Stolyar (1999) and Gamarnik (2004) have established that there exist packing policies under which the average queue size is finite for every ρ ∈ (0, 1). In this paper we study the precise scaling of the average queue size, as a function of ρ, with emphasis on the critical regime where ρ approaches 1. Standard results on the probabilistic (but static) bin-packing problem can be readily applied to produce policies under which the queue size scales as O(h2), where h = 1 / (1 - ρ), which raises the question of whether this is the best possible. We establish that the average queue size scales as Ω(hlogh), under any policy. Furthermore, we provide an easily implementable policy, which packs at most two items per bin. Under that policy, the average queue size scales as O(hlog3/2h), which is nearly optimal. On the other hand, if we impose the additional requirement that any two items packed together must have near-complementary sizes (in a sense to be made precise), we show that the average queue size must scale as Θ(h2).

In this paper we present a dual approximation scheme for the class constrained shelf bin packing problem. In this problem, we are given bins of capacity 1, and n items of Q different classes, each item e with class ce and size se. The problem is to pack the items into bins, such that two items of different classes packed in a same bin must be in different shelves. Items in a same shelf are packed consecutively. Moreover, items in consecutive shelves must be separated by shelf divisors of size d. In a shelf bin packing problem, we have to obtain a shelf packing such that the total size of items and shelf divisors in any bin is at most 1. A dual approximation scheme must obtain a shelf packing of all items into N bins, such that, the total size of all items and shelf divisors packed in any bin is at most 1 + ε for a given ε > 0 and N is the number of bins used in an optimum shelf bin packing problem. Shelf divisors are used to avoid contact between items of different classes and can hold a set of items until a maximum given weight. We also present a dual approximation scheme for the class constrained bin packing problem. In this problem, there is no use of shelf divisors, but each bin uses at most C different classes.

We first motivate and define a notion of asymptoticdifferential approximation ratio. For this, we introduce a new class ofproblems called radial problems including in particular the hereditaryones. Next, we validate the definition of the asymptotic differentialapproximation ratio by proving positive, conditional and negativeapproximation results for some combinatorial problems. We first derive adifferential approximation analysis of a classical greedy algorithm forbin packing, the “first fit decreasing”. Next we deal with minimumvertex-covering-by-cliques of a graph and the minimumedge-covering-by-complete-bipartite-subgraphs of a bipartite graph anddevise a differential-approximation preserving reduction from the formerto the latter. Finally, we prove two negative differential approximationresults about the ability of minimum vertex-coloring to be approximatedby a polynomial time approximation schema.