1 results
Strong Asymptotic Freeness for Free Orthogonal Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 708-720
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
-
It is known that the normalized standard generators of the free orthogonal quantum group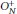
$O_{N}^{+}$ converge in distribution to a free semicircular system as 
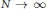$N\,\to \,\infty$. In this note, we substantially improve this convergence result by proving that, in addition to distributional convergence, the operator normof any non-commutative polynomial in the normalized standard generators of 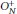$O_{N}^{+}$ converges as 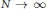$N\,\to \,\infty$ to the operator norm of the corresponding non-commutative polynomial in a standard free semicircular system. Analogous strong convergence results are obtained for the generators of free unitary quantum groups. As applications of these results, we obtain a matrix-coefficient version of our strong convergence theorem, and we recover a well-known 
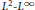${{\mathcal{L}}^{2}}\,-\,{{\mathcal{L}}^{\infty }}$ norm equivalence for noncommutative polynomials in free semicircular systems.
