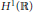Search

In this paper the existence and uniqueness of weak and strong solutions for a non-autonomous non-local reaction–diffusion equation is proved. Furthermore, the existence of minimal pullback attractors in the L2-norm in the frameworks of universes of fixed bounded sets and those given by a tempered growth condition is established, along with some relationships between them. Finally, we prove the existence of minimal pullback attractors in the H1-norm and study relationships among these new families and those given previously in the L2 context. We also present new results in the autonomous framework that ensure the existence of global compact attractors as a particular case.

The existence of the global attractor of a damped forced Hirota equation in the phase space ${{H}^{1}}\left( \mathbb{R} \right)$ is proved. The main idea is to establish the so-called asymptotic compactness property of the solution operator by energy equation approach.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

Time-dependent attractors for non-autonomous non-local reaction–diffusion equations

The Global Attractor of a Damped, Forced Hirota Equation in H1

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

Time-dependent attractors for non-autonomous non-local reaction–diffusion equations

The Global Attractor of a Damped, Forced Hirota Equation in H1