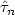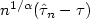1 results
On the minimizing point of the incorrectlycentered empirical process and its limit distributionin nonregular experiments
-
- Journal:
- ESAIM: Probability and Statistics / Volume 9 / February 2005
- Published online by Cambridge University Press:
- 15 November 2005, pp. 307-322
- Print publication:
- February 2005
-
- Article
- Export citation
-
Let F n be the empirical distribution function (df) pertainingto independent random variables with continuous df F. Weinvestigate the minimizing point $\hat\tau_n$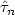
of the empiricalprocess Fn - F0 , where F 0 is another df which differs fromF. If F and F 0 are locally Hölder-continuous of orderα at a point τ our main result states that $n^{1/\alpha}(\hat\tau_n - \tau)$ 
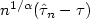converges in distribution. Thelimit variable is the almost sure unique minimizing point of atwo-sided time-transformed homogeneous Poisson-process with adrift. The time-transformation and the drift-function are of thetype |t|α.
