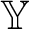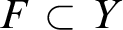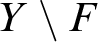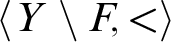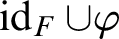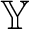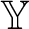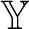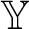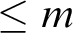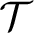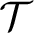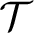A structure 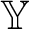 ${\mathbb Y}$
of a relational language L is called almost chainable iff there are a finite set
${\mathbb Y}$
of a relational language L is called almost chainable iff there are a finite set 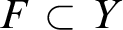 $F \subset Y$
and a linear order
$F \subset Y$
and a linear order  $\,<$
on the set
$\,<$
on the set 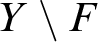 $Y\setminus F$
such that for each partial automorphism
$Y\setminus F$
such that for each partial automorphism 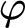 $\varphi $
(i.e., local automorphism, in Fraïssé’s terminology) of the linear order
$\varphi $
(i.e., local automorphism, in Fraïssé’s terminology) of the linear order 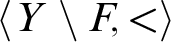 $\langle Y\setminus F, <\rangle $
the mapping
$\langle Y\setminus F, <\rangle $
the mapping 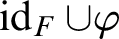 $\mathop {\mathrm {id}}\nolimits _F \cup \varphi $
is a partial automorphism of
$\mathop {\mathrm {id}}\nolimits _F \cup \varphi $
is a partial automorphism of 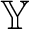 ${\mathbb Y}$
. By theorems of Fraïssé and Pouzet, an infinite structure
${\mathbb Y}$
. By theorems of Fraïssé and Pouzet, an infinite structure 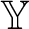 ${\mathbb Y}$
is almost chainable iff the profile of
${\mathbb Y}$
is almost chainable iff the profile of 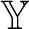 ${\mathbb Y}$
is bounded; namely, iff there is a positive integer m such that
${\mathbb Y}$
is bounded; namely, iff there is a positive integer m such that 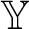 ${\mathbb Y}$
has
${\mathbb Y}$
has 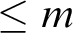 $\leq m$
non-isomorphic substructures of size n, for each positive integer n. A complete first order L-theory
$\leq m$
non-isomorphic substructures of size n, for each positive integer n. A complete first order L-theory 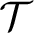 ${\mathcal T}$
having infinite models is called almost chainable iff all models of
${\mathcal T}$
having infinite models is called almost chainable iff all models of 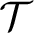 ${\mathcal T}$
are almost chainable and it is shown that the last condition is equivalent to the existence of one countable almost chainable model of
${\mathcal T}$
are almost chainable and it is shown that the last condition is equivalent to the existence of one countable almost chainable model of 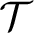 ${\mathcal T}$
. In addition, it is proved that an almost chainable theory has either one or continuum many non-isomorphic countable models and, thus, the Vaught conjecture is confirmed for almost chainable theories.
${\mathcal T}$
. In addition, it is proved that an almost chainable theory has either one or continuum many non-isomorphic countable models and, thus, the Vaught conjecture is confirmed for almost chainable theories.