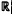Weconsider the Fourier restriction operators associated to certaindegenerate curves in ℝd for which the highest torsion vanishes. We prove estimates with respect to affine arclength and with respect to the Euclidean arclength measure on the curve. The estimates have certain uniform features, and the affine arclength results cover families of flat curves.

The Lp-improving properties of convolution operators with measures supported on space curves have been studied by various authors. If the underlying curve is non-degenerate, the convolution with the (Euclidean) arclength measure is a bounded operator from L3/2(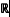)3 into L2(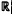3). Drury suggested that in case the underlying curve has degeneracies the appropriate measure to consider should be the affine arclength measure and the obtained a similar result for homogeneous curves t→(t, t2, tk), t >0 for k ≥ 4. This was further generalized by Pan to curves t → (t, tk, tt), t > 0 for l < k < l, k+l ≥ 5. In this article, we will extend Pan's result to (smooth) compact curves of finite type whose tangents never vanish. In addition, we give an example of a flat curve with the same mapping properties.
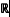