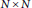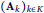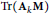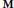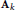For any family of 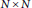$N\,\times \,N$ random matrices 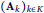${{\left( {{\text{A}}_{k}} \right)}_{k\in K}}$ that is invariant, in law, under unitary conjugation, we give general sufficient conditions for central limit theorems for random variables of the type 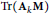$\text{Tr}\left( {{\text{A}}_{k}}\text{M} \right)$, where the matrix 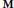$\text{M}$ is deterministic (such random variables include, for example, the normalized matrix entries of 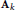${{\text{A}}_{k}}$). A consequence is the asymptotic independence of the projection of the matrices 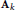${{\text{A}}_{k}}$ onto the subspace of null trace matrices from their projections onto the orthogonal of this subspace. These results are used to study the asymptotic behavior of the outliers of a spiked elliptic random matrix. More precisely, we show that the fluctuations of these outliers around their limits can have various rates of convergence, depending on the Jordan Canonical Form of the additive perturbation. Also, some correlations can arise between outliers at a macroscopic distance from each other.These phenomena have already been observed with random matrices from the Single Ring Theorem.