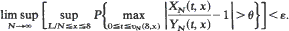1 results
The behavior of the ratio of a small-noise Markov chain to its deterministic approximation
-
- Journal:
- Advances in Applied Probability / Volume 17 / Issue 4 / December 1985
- Published online by Cambridge University Press:
- 01 July 2016, pp. 731-747
- Print publication:
- December 1985
-
- Article
- Export citation
-
For each N≧1, let {XN(t, x), t≧0} be a discrete-time stochastic process with XN(0) = x. Let FN(y) = E(XN(t + 1) | XN(t) = y), and define YN(t, x) = FN(YN(t – 1, x)), t≧1 and YN(0, x) = x. Assume that in a neighborhood of the origin FN(y) = mNy(l + O(y)) where mN> 1, and define for δ> 0 and x> 0, υN(δ, x) = inf{t:xmtN>δ}. Conditions are given under which, for θ> 0 and ε> 0, there exist constants δ > 0 and L <∞, depending on εand 0, such that
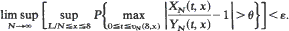This result together with a result of Kurtz (1970), (1971) shows that, under appropriate conditions, the time needed for the stochastic process {XN(t, 1/N), t≧0} to escape a δ -neighborhood of the origin is of order log Νδ /log mN. To illustrate the results the Wright-Fisher model with selection is considered.
