We use axioms of abstract ternary relations to define the notion of a free amalgamation theory. These form a subclass of first-order theories, without the strict order property, encompassing many prominent examples of countable structures in relational languages, in which the class of algebraically closed substructures is closed under free amalgamation. We show that any free amalgamation theory has elimination of hyperimaginaries and weak elimination of imaginaries. With this result, we use several families of well-known homogeneous structures to give new examples of rosy theories. We then prove that, for free amalgamation theories, simplicity coincides with NTP2 and, assuming modularity, with NSOP3 as well. We also show that any simple free amalgamation theory is 1-based. Finally, we prove a combinatorial characterization of simplicity for Fraïssé limits with free amalgamation, which provides new context for the fact that the generic Kn-free graphs are SOP3, while the higher arity generic 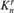$K_n^r$-free r-hypergraphs are simple.

We compare distributions of residual lifetimes of dependent components of different age. This approach yields several notions of multivariate ageing. A special feature of our notions is that they are based on one-dimensional stochastic comparisons. Another difference from the traditional approach is that we do not condition on different histories.

Some concepts of dependence have recently been introduced by Ebrahimi (1987) to explore the structural properties of the hitting times of bivariate processes. In this framework, the special case of univariate processes has curious features. New properties are derived for this case. Some applications to sequential inference and inequalities for Brownian motion and new better than used (NBU) processes are also provided.