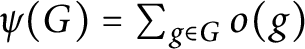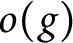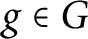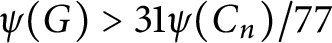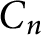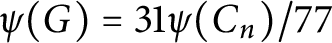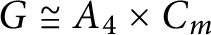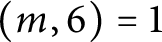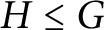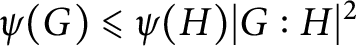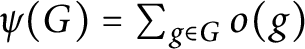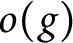Let G be a finite group and $\psi (G) = \sum _{g \in G} o(g)$ , where $o(g)$ denotes the order of 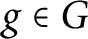$g \in G$ . There are many results on the influence of this function on the structure of a finite group G.

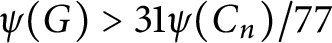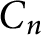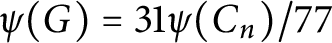In this paper, as the main result, we answer a conjecture of Tărnăuceanu. In fact, we prove that if G is a group of order n and $\psi (G)>31\psi (C_n)/77$ , where $C_n$ is the cyclic group of order n, then G is supersolvable. Also, we prove that if G is not a supersolvable group of order n and $\psi (G) = 31\psi (C_n)/77$ , then 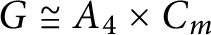$G\cong A_4 \times C_m$ , where 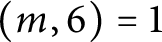$(m, 6)=1$ .

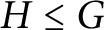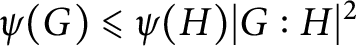Finally, Herzog et al. in (2018, J. Algebra, 511, 215–226) posed the following conjecture: If $H\leq G$ , then $\psi (G) \unicode[stix]{x02A7D} \psi (H) |G:H|^2$ . By an example, we show that this conjecture is not satisfied in general.