1 results
Magnitude and Holmes–Thompson intrinsic volumes of convex bodies
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 854-867
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
Magnitude is a numerical invariant of compact metric spaces, originally inspired by category theory and now known to be related to myriad other geometric quantities. Generalizing earlier results in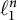
$\ell _1^n$ and Euclidean space, we prove an upper bound for the magnitude of a convex body in a hypermetric normed space in terms of its Holmes–Thompson intrinsic volumes. As applications of this bound, we give short new proofs of Mahler’s conjecture in the case of a zonoid and Sudakov’s minoration inequality.
