1 results
Stieltjes classes for moment-indeterminate probability distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue A / 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 281-294
- Print publication:
- 2004
-
- Article
- Export citation
-
Let F be a probability distribution function with density f. We assume that (a) F has finite moments of any integer positive order and (b) the classical problem of moments for F has a nonunique solution (F is M-indeterminate). Our goal is to describe a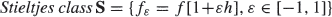
, where h is a ‘small' perturbation function. Such a class S consists of different distributions Fε (fε is the density of Fε) all sharing the same moments as those of F, thus illustrating the nonuniqueness of F, and of any Fε, in terms of the moments. Power transformations of distributions such as the normal, log-normal and exponential are considered and for them Stieltjes classes written explicitly. We define a characteristic of S called an index of dissimilarity and calculate its value in some cases. A new Stieltjes class involving a power of the normal distribution is presented. An open question about the inverse Gaussian distribution is formulated. Related topics are briefly discussed.
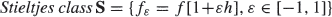, where 