1 results
Limits of compound and thinned point processes
-
- Journal:
- Journal of Applied Probability / Volume 12 / Issue 2 / June 1975
- Published online by Cambridge University Press:
- 14 July 2016, pp. 269-278
- Print publication:
- June 1975
-
- Article
- Export citation
-
Let η =Σjδτj be a point process on some space S and let β,β1,β2, … be identically distributed non-negative random variables which are mutually independent and independent of η. We can then form the compound point process ξ = Σjβjδτj which is a random measure on S. The purpose of this paper is to study the limiting behaviour of ξ as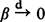
. In the particular case when β takes the values 1 and 0 with probabilities p and 1 –p respectively, ξ becomes a p-thinning of η and our theorems contain some classical results by Rényi and others on the thinnings of a fixed process, as well as a characterization by Mecke of the class of subordinated Poisson processes.
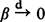. In the particular case when 