We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We obtain asymptotic formulas for the number of matrices in the congruence subgroup 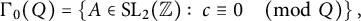which are of naive height at most X. Our result is uniform in a very broad range of values Q and X.
$$\begin{align*}\Gamma_0(Q) = \left\{ A\in\operatorname{SL}_2({\mathbb Z}):~c \equiv 0 \quad\pmod Q\right\}, \end{align*}$$
