We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the long-standing problem of the existence of non-Berwaldian Landsberg spaces from the perspective of conformal transformations. We calculate the Berwald and Landsberg tensors in terms of the T-tensor and show that there are Landsberg spaces with nonvanishing T-tensor. We give a necessary condition for a Landsberg space to be Berwaldian. We find conditions under which the Landsberg spaces cannot be Berwaldian and give examples of (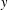
$y$-local) non-Berwaldian Landsberg spaces.
