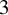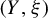We develop a forcing theory of topological entropy for Reeb flows in dimension three. A transverse link L in a closed contact $3$ -manifold $(Y,\xi )$ is said to force topological entropy if 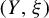$(Y,\xi )$ admits a Reeb flow with vanishing topological entropy, and every Reeb flow on 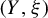$(Y,\xi )$ realizing L as a set of periodic Reeb orbits has positive topological entropy. Our main results establish topological conditions on a transverse link L, which imply that L forces topological entropy. These conditions are formulated in terms of two Floer theoretical invariants: the cylindrical contact homology on the complement of transverse links introduced by Momin [A. Momin. J. Mod. Dyn.5 (2011), 409–472], and the strip Legendrian contact homology on the complement of transverse links, introduced by Alves [M. R. R. Alves. PhD Thesis, Université Libre de Bruxelles, 2014] and further developed here. We then use these results to show that on every closed contact 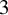$3$ -manifold that admits a Reeb flow with vanishing topological entropy, there exist transverse knots that force topological entropy.

We construct a dynamically convex contact form on the three-sphere whose systolic ratio is arbitrarily close to 2. This example is related to a conjecture of Viterbo, whose validity would imply that the systolic ratio of a convex contact form does not exceed 1. We also construct, for every integer $n\geqslant 2$, a tight contact form with systolic ratio arbitrarily close to $n$ and with suitable bounds on the mean rotation number of all the closed orbits of the induced Reeb flow.