Let U be the distribution function of the passage time of an individual bond of the square lattice, and let pT be the critical probability above which the expected size of the open component of the origin (in the usual bond percolation) is infinite. It is shown that if (∗)U(0–) = 0, U(0) < pT, then there exist constants 0 < a, C1 < ∞ such that 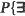 a self-avoiding path of at least n steps starting at the origin and with passage time ≦ an} ≦ 2 exp (–C1n).
a self-avoiding path of at least n steps starting at the origin and with passage time ≦ an} ≦ 2 exp (–C1n).
From this it follows that under (∗) the time constant μ (U) of first-passage percolation is strictly positive and that for each c > 0 lim sup (1/n)Nn(c) <∞, where Nn(c) is the maximal number of steps in the paths starting at the origin with passage time at most cn.

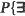 a self-avoiding path of at least
a self-avoiding path of at least 