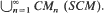1 results
Classes of probability density functions having Laplace transforms with negative zeros and poles
-
- Journal:
- Advances in Applied Probability / Volume 19 / Issue 3 / September 1987
- Published online by Cambridge University Press:
- 01 July 2016, pp. 632-651
- Print publication:
- September 1987
-
- Article
- Export citation
-
We consider a class of functions on [0,∞), denoted by Ω, having Laplace transforms with only negative zeros and poles. Of special interest is the class Ω+ of probability density functions in Ω. Simple and useful conditions are given for necessity and sufficiency of f ∊ Ω to be in Ω+. The class Ω+ contains many classes of great importance such as mixtures of n independent exponential random variables (CMn), sums of n independent exponential random variables (PF∗n), sums of two independent random variables, one in CMr and the other in PF∗1 (CMPFn with n = r + l) and sums of independent random variables in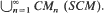
CMn(SCM). Characterization theorems for these classes are given in terms of zeros and poles of Laplace transforms. The prevalence of these classes in applied probability models of practical importance is demonstrated. In particular, sufficient conditions are given for complete monotonicity and unimodality of modified renewal densities.
