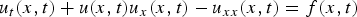We study the non-autonomously forced Burgers equation
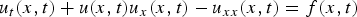 $$u_t(x,t) + u(x,t)u_x(x,t)-u_{xx}(x,t) = f(x,t)$$
$$u_t(x,t) + u(x,t)u_x(x,t)-u_{xx}(x,t) = f(x,t)$$