We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let X be a Banach space, D an open subset of X and Y a complete metric space. Assume that Y is metrically convex. For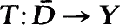 
closed, locally m-expansive and mapping open subsets of D onto open subsets of Y, is is shown that y ∊ T(D) if and only if there exists x0 ∊ D such that d(Tx0, y) ≤ d(Tx, y) for all x ≤ ∂D.
