An analytic function f in the unit disc 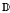belongs to F(p,q,s), if

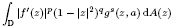
is uniformly bounded for all a ∈ 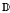. Here 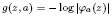is the Green function of 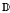, and φa(z)=(a−z)/(1−āz). It is shown that for 0 < γ < ∞ and |w|=1 the singular inner function exp(γ(z+w)/(z−w)) belongs to F(p,q,s), 0<s≤1, if and only if 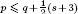. Moreover, it is proved that, if 0<s<1, then an inner function belongs to the Möbius invariant Besov-type space 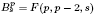for some (equivalently for all) p > max{s,1−s} if and only if it is a Blaschke product whose zero sequence {zn} satisfies .

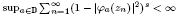We study the membership of Blaschke products in Lipschitz spaces, especially for interpolating Blaschke products and for those whose zeros lie in a Stolz angle. We prove several theorems that complement or extend the earlier works of Ahern and the author.

We study the membership of derivatives of Blaschke products in Hardy and Bergman spaces, especially for the the interpolating Blaschke products and for those whose zeros lie in a Stolz domain. We obtain new and very simple proofs of some known results and prove new theorems that complement or extend the earlier works of Ahern, Clark, Cohn, Kim, Newman, Protas, Rudin, Vinogradov and others.