1 results
LEARNING THEORY IN THE ARITHMETIC HIERARCHY
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 18 August 2014, pp. 908-927
- Print publication:
- September 2014
-
- Article
- Export citation
-
We consider the arithmetic complexity of index sets of uniformly computably enumerable families learnable under different learning criteria. We determine the exact complexity of these sets for the standard notions of finite learning, learning in the limit, behaviorally correct learning and anomalous learning in the limit. In proving the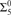
${\rm{\Sigma }}_5^0$-completeness result for behaviorally correct learning we prove a result of independent interest; if a uniformly computably enumerable family is not learnable, then for any computable learner there is a 
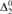${\rm{\Delta }}_2^0$ enumeration witnessing failure.
