Let {Sn, n ≧ 1} be a zero, mean square integrable martingale for which 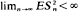 so that Sn → S∞ a.s., say, by the martingale convergence theorem. The paper is principally concerned with obtaining central limit and iterated logarithm results for Bn(Sn – S∞) where the multipliers Bn ↑ ∞ a.s. An example on the Pólya urn scheme is given to illustrate the results.
so that Sn → S∞ a.s., say, by the martingale convergence theorem. The paper is principally concerned with obtaining central limit and iterated logarithm results for Bn(Sn – S∞) where the multipliers Bn ↑ ∞ a.s. An example on the Pólya urn scheme is given to illustrate the results.