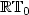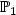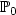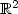We present a new stabilized mixed finite element method for the linear elasticity problem in $\mathbb{R}^2$ 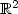 . Theapproach is based on the introduction of Galerkin least-squares terms arising from the constitutive andequilibrium equations, and from the relation defining the rotation in terms of the displacement. We show thatthe resulting augmented variational formulation and the associated Galerkin scheme are well posed, and thatthe latter becomes locking-free and asymptotically locking-free for Dirichlet and mixed boundary conditions,respectively. In particular, the discrete scheme allows the utilization of Raviart–Thomas spaces of lowestorder for the stress tensor, piecewise linear elements for the displacement, and piecewise constants for therotation. In the case of mixed boundary conditions, the essential one (Neumann) is imposed weakly, whichyields the introduction of the trace of the displacement as a suitable Lagrange multiplier. This trace isthen approximated by piecewise linear elements on an independent partition of the Neumann boundary whose meshsize needs to satisfy a compatibility condition with the mesh size associated to the triangulation of thedomain. Several numerical results illustrating the good performance of the augmented mixed finite elementscheme in the case of Dirichlet boundary conditions are also reported.
. Theapproach is based on the introduction of Galerkin least-squares terms arising from the constitutive andequilibrium equations, and from the relation defining the rotation in terms of the displacement. We show thatthe resulting augmented variational formulation and the associated Galerkin scheme are well posed, and thatthe latter becomes locking-free and asymptotically locking-free for Dirichlet and mixed boundary conditions,respectively. In particular, the discrete scheme allows the utilization of Raviart–Thomas spaces of lowestorder for the stress tensor, piecewise linear elements for the displacement, and piecewise constants for therotation. In the case of mixed boundary conditions, the essential one (Neumann) is imposed weakly, whichyields the introduction of the trace of the displacement as a suitable Lagrange multiplier. This trace isthen approximated by piecewise linear elements on an independent partition of the Neumann boundary whose meshsize needs to satisfy a compatibility condition with the mesh size associated to the triangulation of thedomain. Several numerical results illustrating the good performance of the augmented mixed finite elementscheme in the case of Dirichlet boundary conditions are also reported.
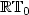 - $\mathbb{P}_1$
- $\mathbb{P}_1$ 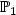 - $\mathbb{P}_0$
- $\mathbb{P}_0$ 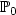 approximations
approximations