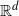1 results
A deep look into the dagum family of isotropic covariance functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 August 2022, pp. 1026-1041
- Print publication:
- December 2022
-
- Article
- Export citation
-
The Dagum family of isotropic covariance functions has two parameters that allow for decoupling of the fractal dimension and the Hurst effect for Gaussian random fields that are stationary and isotropic over Euclidean spaces. Sufficient conditions that allow for positive definiteness in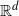
$\mathbb{R}^d$
of the Dagum family have been proposed on the basis of the fact that the Dagum family allows for complete monotonicity under some parameter restrictions. The spectral properties of the Dagum family have been inspected to a very limited extent only, and this paper gives insight into this direction. Specifically, we study finite and asymptotic properties of the isotropic spectral density (intended as the Hankel transform) of the Dagum model. Also, we establish some closed-form expressions for the Dagum spectral density in terms of the Fox–Wright functions. Finally, we provide asymptotic properties for such a class of spectral densities.
