Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

3 results

  • Homogeneous and curvature homogeneous Lorentzian critical metrics

  • Part of
  • M. Brozos-Vázquez, S. Caeiro-Oliveira, E. García-Río
  • Journal:
    Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
    Published online by Cambridge University Press:
    08 July 2022, pp. 1272-1296
    Print publication:
    August 2023
    • Article
      • You have access
      • Open access
    • PDF
    • HTML
    • Export citation

  • We determine all three-dimensional homogeneous and $1$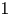-curvature homogeneous Lorentzian metrics which are critical for a quadratic curvature functional. As a result, we show that any quadratic curvature functional admits different non-Einstein homogeneous critical metrics and that there exist homogeneous metrics which are critical for all quadratic curvature functionals without being Einstein.

  • 4 - Overview of Mathematical Tools

  • from Part I - Fundamentals
  • Marco Tartagni, University of Bologna
  • Book:
    Electronic Sensor Design Principles
    Published online:
    23 December 2021
    Print publication:
    06 January 2022, pp 189-235

  • Summary

    This chapter gives a short summary of mathematical instruments required to model sensor systems in the presence of both deterministic and random processes. The concepts are organized in a compact overview for a more rapid consultation, emphasizing the convergences between different contexts.

  • 6 - The Origin of Noise

  • from Part II - Noise and Electronic Interfaces
  • Marco Tartagni, University of Bologna
  • Book:
    Electronic Sensor Design Principles
    Published online:
    23 December 2021
    Print publication:
    06 January 2022, pp 251-312

  • Summary

    Understanding the origin of noise is important because it gives hints on how to reduce its effects even from the electronic point of view. This chapter analyzes the physics background of some sources of random processes that are limiting sensing systems referred to as “thermal,” “shot,” and “flicker” noises. It also shows how thermal and shot noises are at the base of other observed electronic effects such as “kTC,” “phase,” and “current” noises. The discussion uses analogies between mechanical and electronic effects of thermal agitation. This is important not only for understanding the process but also to unify the model of noise in microelectromechanical sensor systems so as to use the same analysis framework.