1 results
AN EIGENSPACE OF LARGE DIMENSION FOR A HECKE ALGEBRA ON AN
BUILDING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 29-54
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
-
Let Δ be an affine building of type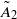
and let 𝔸 be its fundamental apartment. We consider the set 𝕌0 of vertices of type 0 of 𝔸 and prove that the Hecke algebra of all W0-invariant difference operators with constant coefficients acting on 𝕌0 has three generators. This property leads us to define three Laplace operators on vertices of type 0 of Δ. We prove that there exists a joint eigenspace of these operators having dimension greater than ∣W0 ∣. This implies that there exist joint eigenfunctions of the Laplacians that cannot be expressed, via the Poisson transform, in terms of a finitely additive measure on the maximal boundary Ω of Δ.
BUILDING
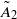and let 𝔸 be its fundamental apartment. We consider the set 𝕌