We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Starting points of this article are fixed point axioms for set-bounded monotone Σ1 definable operators in the context of Kripke–Platek set theory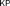 
$KP$. We analyze their relationship to other principles such as maximal iterations, bounded proper injections, and Σ1 subset-bounded separation. One of our main results states that in 
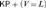$KP + (V\, = \,L)$ all these principles are equivalent to Σ1 separation.
