We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We set out some general criteria to prove the K-property, refining the assumptions used in an earlier paper for the flow case, and introducing the analogous discrete-time result. We also introduce one-sided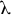 
$\lambda $
-decompositions, as well as multiple techniques for checking the pressure gap required to show the K-property. We apply our results to the family of Mañé diffeomorphisms and the Katok map. Our argument builds on the orbit decomposition theory of Climenhaga and Thompson.
