We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study a class of optimal transport planning problems where the reference cost involves a non-linear function G(x, p) representing the transport cost between the Dirac measure δx and a target probability p. This allows to consider interesting models which favour multi-valued transport maps in contrast with the classical linear case (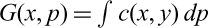
$G(x,p)=\int c(x,y)dp$) where finding single-valued optimal transport is a key issue. We present an existence result and a general duality principle which apply to many examples. Moreover, under a suitable subadditivity condition, we derive a Kantorovich–Rubinstein version of the dual problem allowing to show existence in some regular cases. We also consider the well studied case of Martingale transport and present some new perspectives for the existence of dual solutions in connection with Γ-convergence theory.
