The Jucys–Murphy elements for wreath products $\Gamma_n = \Gamma \wr S_n $ associated to any finite group $\Gamma$ are introduced and they play an important role in our study of the connections between class algebras of $\Gamma_n$ for all $n$ and vertex algebras. We construct an action of (a variant of) the $\mathcal W_{1 + \infty}$-algebra acting irreducibly on the direct sum ${\mathcal R}_\Gamma$ of the class algebras of $\Gamma_n$ for all $n$ in a group-theoretic manner. We establish various relations between convolution operators using JM elements and Heisenberg algebra operators acting on ${\mathcal R}_\Gamma$. As applications, we obtain two distinct sets of algebra generators for the class algebra of $\Gamma_n$ and establish various stability results concerning products of normalized conjugacy classes of $\Gamma_n$ and the power sums of Jucys--Murphy elements, etc. We introduce a stable algebra which encodes the class algebra structures of $\Gamma_n$ for all $n$, whose structure constants are shown to be non-negative integers. In the symmetric group case (that is, when $\Gamma$ is trivial), we recover and strengthen in a uniform approach various results of Lascoux and Thibon, Kerov and Olshanski, and Farahat and Higman, etc.

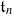 . We show that Gaudin subalgebras form a variety isomorphic to the moduli space
. We show that Gaudin subalgebras form a variety isomorphic to the moduli space 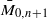 of stable curves of genus zero with
of stable curves of genus zero with 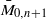 in a Grassmannian of (
in a Grassmannian of (