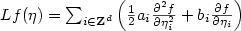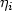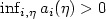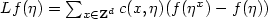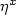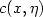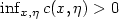Consider an infinite dimensionaldiffusion process process on TZd, whereT is the circle, defined by the action of its generatorL on C2(TZd) local functions as$Lf(\eta)=\sum_{i\in{\bf Z}^d}\left(\frac{1}{2}a_i\frac{\partial^2 f}{\partial \eta_i^2}+b_i\frac{\partial f}{\partial \eta_i}\right)$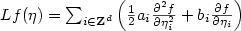 . Assume that the coefficients, ai and bi are smooth,bounded, finite range with uniformly bounded second orderpartial derivatives, that ai is only a function of $\eta_i$
. Assume that the coefficients, ai and bi are smooth,bounded, finite range with uniformly bounded second orderpartial derivatives, that ai is only a function of $\eta_i$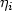 and that $\inf_{i,\eta}a_i(\eta)>0$
and that $\inf_{i,\eta}a_i(\eta)>0$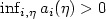 .Suppose ν is an invariant product measure. Then,if ν is the Lebesgue measure or if d=1,2, it is theunique invariant measure. Furthermore, if ν istranslation invariant, then it is the unique invariant, translationinvariant measure. Now, consider an infinite particlespin system, with state space {0,1}Zd, definedby the action of its generator on local functions f by$Lf(\eta)=\sum_{x\in{\bf Z}^d}c(x,\eta)(f(\eta^x)-f(\eta))$
.Suppose ν is an invariant product measure. Then,if ν is the Lebesgue measure or if d=1,2, it is theunique invariant measure. Furthermore, if ν istranslation invariant, then it is the unique invariant, translationinvariant measure. Now, consider an infinite particlespin system, with state space {0,1}Zd, definedby the action of its generator on local functions f by$Lf(\eta)=\sum_{x\in{\bf Z}^d}c(x,\eta)(f(\eta^x)-f(\eta))$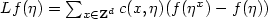 ,where $\eta^x$
,where $\eta^x$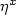 is the configuration obtained from ηaltering only the coordinate at site x. Assume that $c(x,\eta)$
is the configuration obtained from ηaltering only the coordinate at site x. Assume that $c(x,\eta)$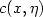 are of finite range, bounded and that $\inf_{x,\eta}c(x,\eta)>0$
are of finite range, bounded and that $\inf_{x,\eta}c(x,\eta)>0$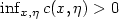 .Then, if ν is an invariant product measure for this process,ν is unique when d=1,2. Furthermore, if ν is translationinvariant, it is the unique invariant, translation invariantmeasure. The proofs of these results show how elementarymethods can give interesting information for general processes.
.Then, if ν is an invariant product measure for this process,ν is unique when d=1,2. Furthermore, if ν is translationinvariant, it is the unique invariant, translation invariantmeasure. The proofs of these results show how elementarymethods can give interesting information for general processes.