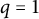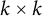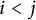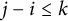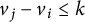Immanants are functions on square matrices generalizing the determinant and permanent. Kazhdan–Lusztig immanants, which are indexed by permutations, involve 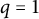$q=1$ specializations of Type A Kazhdan–Lusztig polynomials, and were defined by Rhoades and Skandera (2006, Journal of Algebra 304, 793–811). Using results of Haiman (1993, Journal of the American Mathematical Society 6, 569–595) and Stembridge (1991, Bulletin of the London Mathematical Society 23, 422–428), Rhoades and Skandera showed that Kazhdan–Lusztig immanants are nonnegative on matrices whose minors are nonnegative. 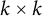We investigate which Kazhdan–Lusztig immanants are positive on k-positive matrices (matrices whose minors of size $k \times k$ and smaller are positive). 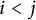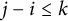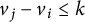The Kazhdan–Lusztig immanant indexed by v is positive on k-positive matrices if v avoids 1324 and 2143 and for all noninversions $i< j$ of v, either $j-i \leq k$ or $v_j-v_i \leq k$ . Our main tool is Lewis Carroll’s identity.