We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the problem : (P) Minimize $\lambda _{2}$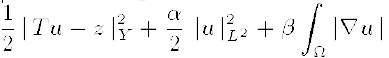 
over u ∈ K ∩ X, where α≥ 0, β > 0, K is a closed convex subset of L 2(Ω), and the last additive term denotes the BV-seminorm of u, T is a linear operator from L 2 ∩ BV into the observation space Y. We formulate necessary optimality conditions for (P). Then we show that (P) admits, for givenregularization parameters α and β, solutions which depend in a stable manner on the data z. Finally we study the asymptotic behavior when α = β → 0. The regularized solutions ûβ of (P) converge to the L 2 ∩ BV minimal norm solution of the unregularized problem. The rate of convergence is β½ when the minimum-norm solution û is smooth enough.
